金融市場是個多元複雜又規模巨大的場域,許多學者都試圖用方便理解的譬喻來幫助人們掌握核心概念。當然,模型必然與實際本體有些差距,但立論精確的數學譬喻,能化約看似難解的龐大變數,進而標定出關鍵要素,增進我們對市場的認識。今天要談的,就是用一個簡單的遊戲,來展現股市難以預測的本質:猜數字遊戲(number guessing game)
猜數字遊戲淵源已久,歷史上有不同版本,最先提出的人眾說紛紜,這裡以Richard Thaler教授1997年於英國金融時報上進行的經典實驗來介紹。
遊戲規則很簡單:
0到100間猜一個整數,該數字最接近「所有參與者所提數字之平均值的2/3」獲勝。
舉例:
A猜10、B猜40、C猜70,則(10+40+70)/3=40,而40*(2/3)=26.666
B猜40最接近26,故獲勝
有興趣的讀者可以找朋友或是自己隨機喊幾個數字來玩玩看,看結果會如何。準備好揭曉答案了嗎?
有興趣的讀者可以找朋友或是自己隨機喊幾個數字來玩玩看,看結果會如何。準備好揭曉答案了嗎?
嗯,沒有標準答案。
接著我們就來拆解這個遊戲的寓意。
--
一個普通玩家,可能覺得這個問題很複雜或是懶得猜,因此就從0到100間隨機選擇一個數字。他沒有對問題進行任何推斷,這裡將其定義為零級參與者。
如果稍微推理,假設其他玩家都是零級參與者,而樣本夠大的話,那麼許多人在0到100間隨機選擇,其平均值應為50。因此想要獲勝,就應該猜50的2/3,也就是33.333(取整數33)。由於此時對其他人的選擇進行了一次推理,因此這樣的玩家將其定義為一級參與者。
如果玩家都能想到這一步,那麼所有參與者都會猜33,但此時所有人選擇數字之平均值的2/3就會變成22。此時的答案,就從33變成了22。這些進行兩次推理的玩家,將其定義為二級參與者。
但是,如果所有的玩家都夠聰明成了二級參與者,那麼正解又從22變成了14.666(取整數15)。這些進行三次推理的玩家,將其定義為三級參與者。
如果所有人又推測到這一步,那麼大家都會選擇15,此時最佳解又變成15的2/3,成為10了。這些進行四次推理的玩家,將其定義為四級參與者。
如果大家都非常聰明(心機重),那麼不斷推理下去,成為五級、六級、十級,一百級參與者,最佳解可想見也會越來越小。
視覺化來看:
視覺化來看:
0級:50
1級:50*(2/3)=33
2級:50*(2/3)*(2/3)=22
3級:50*(2/3)*(2/3)*(2/3)=15
4級:50*(2/3)*(2/3)*(2/3)*(2/3)=10
~
這個層次可以持續推論下去。令題目設定之數字範圍0至100,則整個推理過程寫成算式,即為100不斷乘以2/3,最終會無限趨近於0。寫到這邊,我們整理一下思緒。
這個遊戲參與者眾多,且每個人決策會相互影響,沒有參與者可以「獨自行動」(單方面改變決定)來增加收穫。如果所有參與者都遵循相同策略而達到最優選擇,此時,一個關鍵概念浮現了:這個策略組合就稱為奈許均衡(Nash Equilibrium)。猜數字遊戲中,如果所有人都選擇0,那麼就能保證所有人穩定獲勝,0就是奈許均衡。
這個層次可以持續推論下去。令題目設定之數字範圍0至100,則整個推理過程寫成算式,即為100不斷乘以2/3,最終會無限趨近於0。寫到這邊,我們整理一下思緒。
這個遊戲參與者眾多,且每個人決策會相互影響,沒有參與者可以「獨自行動」(單方面改變決定)來增加收穫。如果所有參與者都遵循相同策略而達到最優選擇,此時,一個關鍵概念浮現了:這個策略組合就稱為奈許均衡(Nash Equilibrium)。猜數字遊戲中,如果所有人都選擇0,那麼就能保證所有人穩定獲勝,0就是奈許均衡。
然而問題是,世界上並沒有那麼多天才。即使是非常聰明的參與者,也需要考慮其他參與者是否能找到奈許均衡。因此,即便是已經找到奈許均衡的參與者,他所給出的答案就不一定是奈許均衡了。此時的問題就變成:其他參與者會考慮到哪一步?
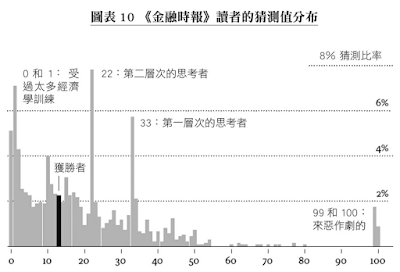
回到Thaler的實驗,金融時報調查的結果是13。
(延伸閱讀 不當行為:行為經濟學之父教你更聰明的思考、理財、看世界)
從統計圖看到,金融時報讀者群具備一定數學程度,許多人選擇奈許均衡點0或是接近0的1,但他們卻忽略了並非所有人都能找到奈許均衡,因此,直接選擇0或1並不是最佳解。有人隨機猜,有人思考層級不深,甚至還有人故意猜極高極低來擾亂答案;你知道你的對手是哪些人嗎?這種決策路徑混沌不明的狀況下,正確答案,很沒把握。
寫到這邊,這個遊戲的寓意就呼之欲出了:「你的選擇」會因為「眾人的選擇」而成功或失敗。
--
複雜理論(Complexity Theory)在這裡值得援引。複雜理論的核心論述是系統變化難以預測。一階複雜系統指的是,人為預測不會改變現象的結果(如氣象學家預測到颱風路徑,但颱風這個自然現象不會因為人為預測而有所變化)。二階複雜系統指的是,人為預測會改變現象結果,也就是猜數字遊戲案例中,每個人猜的數字不同會對最佳解造成變化。
這個遊戲可以用Howard Marks的第二層思考來探討,但依然會面臨到對手怎麼想的困境。你有思考嗎?你所思考的層次夠深嗎?你考慮到其他對手的思考了嗎?你有沒有可能想太多,聰明反被聰明誤?層次太多了,筆者個人比較喜歡用鏡花水月的概念來理解。(懂梗的人請舉手)
猜數字遊戲經常跟凱因斯報紙選美譬喻連帶出現,意思大同小異。如果要獲得勝利,那麼參與者要選的不是自己覺得最好的,而是大家覺得最好看的。也就是說,我們要去猜測別人會怎麼選。
把寓意寫成通俗語言,意思就是,買股票與其說是選擇自己覺得最有價值的股票,毋寧說是選擇市場認為最有價值的股票。如果你真的能知道整個市場在想什麼,那麼無論市場想法多麼荒謬,你都可以利用市場的想法賺錢。因此,股票市場這種選美遊戲,就是一個你與整個市場(所有參與者加總)的博弈。
有人贏過市場,必然有人會輸給市場,因為市場就是所有人績效的加總平均。想要贏過市場,就是進行零和遊戲。
面對這個賽局,投資者可以用被動追蹤市場指數的基金來參與,當本身成為市場,至少能保證自己不會落後標竿(而且根據本網誌多次提及的SPIVA統計,長期持有S&P500就能勝過近八成的參與者)。跟著市場同步成長,不需要擊敗誰,就能跟著實體經濟一同成長。或者投資者也可以主動參與,試圖找出在賽局中贏過他人的方式,這也是各種投資策略的殘酷競技場。賽局理論有許多延伸與變體情境(如重複賽局),某種程度上或許有打敗對手的算式,也是主動投資派夢寐以求的聖杯。
筆者目前的思考邏輯(也是本網誌名稱的彩蛋)是在機率中追求正期望值。我不求猜到精準的數字,但只要範圍「約略正確」,長久累積下來期望值是正的,績效就能持續成長。
寫到最後,回到本文所推論的核心概念:「你的選擇」會因為「眾人的選擇」而成功或失敗。這個概念不難理解,人生中很多事物也呈現這樣的賽局。謹記這個簡單的概念,就能提醒自己身處更加複雜的股市時,就算決策充滿自信,也很有可能遇上意料之外的失敗。
如同Ken Fisher在其著作一再提到,市場是個大羞辱者(The Great Humiliator),經常讓滿懷自信的投資人出糗,這點也呼應到猜數字遊戲所透露的市場本質。因此,常保謙虛不只是道德上的禮貌,看來也挺有數理實際上的必要性(笑)。

沒有留言:
張貼留言